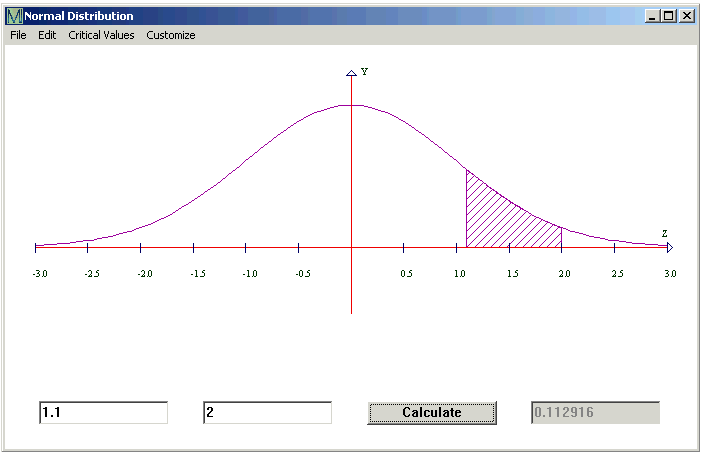
CalGraph will calculate the area under the bell curve, that is, the chance that a standard normal variable lies between two values.
Click on Statistics at the top of the window and then on Normal Distribution. This window opens.

Type the lower number in the first box and the higher in the second box. Then click Calculate.
Here CalGraph shows that the chance a standard normal variable is between 1.1 and 2 is 0.112916.
The graph shows the area under the bell curve shaded.
You may want the area below some value, say z < 2, which means minus infinity < z < 2. Because the curve is so close to the axis, you can put -5 (or any number below -5) in the left box. To six decimal places there is no difference in the area.
If you want the area above some value, maybe z > 1.1
This means 1.1 < z < infinity. Put 5 (or any number above 5) in the second box. The area will be correct to six decimal places.
You can print the graph and your result by clicking File and then Print. Or you can copy it to another document, using Edit > Copy Graph to Clipboard and then Paste in that document.
CalGraph will also calculate the other way,
Given an area, CalGraph will find the z-value which cuts off that area. At the top of the Normal Distribution window, click on Critical Values and then Alpha.
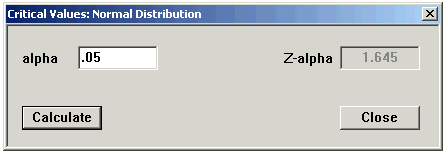
Put the area you know in the alpha box and click Calculate.
I put in .05 That 0.05 is the area of the region under the bell curve between 1.645 and infinity.
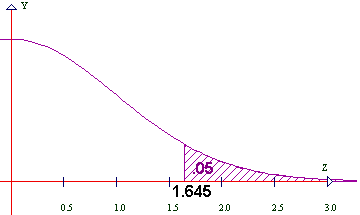
Maybe the diagram makes the idea clearer.
You may want a probability bigger than 50% = 0.5
The Normal Distribution graph is symmetric. The vertical line cuts the bell in half, 0.5 on each side. So the z you want will be negative. To get this value, put one minus the area you want in the Alpha box, and make the answer negative.
Here's one done out: I wanted 0.9 to be the area under the curve.
1 - 0.9 = 0.1 so I put .1 in the Alpha box.
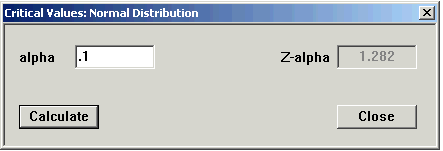
Now I make the z negative: the critical value of z = -1.282 Here's the graph of what happened.
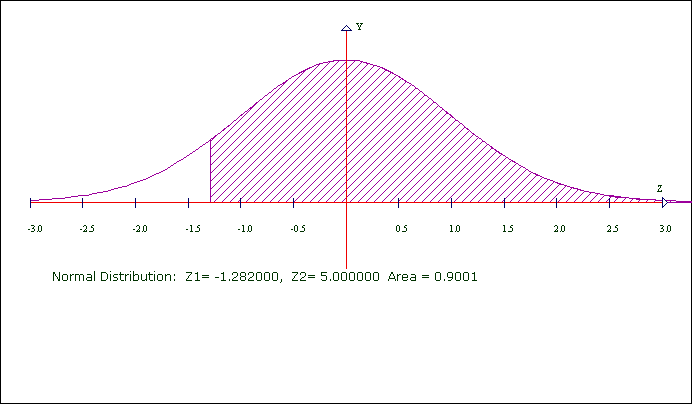
You can see the area is not exactly 0.9. This is round-off error.
CalGraph will calculate the p-value for a hypothesis test.