Separating Objects in Space
INTRODUCTION
A recurring problem in computer graphics and robot motion planning is to determine if
objects can be separated without colliding. In a video game, one needs to move
representations of people and machines without their images overlapping. An explosion can
be depicted on screen as a simultaneous separation of particles. One may wish to send a
robot through a field of obstacles.
There are many variations within this class of problems. Aside from rare examples such
as the sofa problem in which one attempts to specify the shape of an object which must
follow a specified trajectory, most published problems pertain to moving objects which are
restricted to, for example, spheres, isothetic rectangles, smooth convex bodies, convex
polygons or star-shaped polygons. The motion is often limited to translations and
sometimes only to translations parallel to a given line or set of axes. One might inquire
whether a single object can be perturbed without disturbing the others or investigate if
an object can be moved as far apart from the others as desired. Some collections of
objects can only be separated sequentially, others only if subgroups are first separated
and still others only if all are set in motion simultaneously. The answers can vary with
the dimension of the space in which the objects reside. By a theorem of Dawson, any
collection of more than two smooth convex objects in R2 can be separated, but
counter-examples exist to the analogous theorem for R3.
The solutions of the above problems engender many more problems. Having determined
theoretically that any collection of a particular class of objects possesses a particular
type of separability, one might still need to develop an efficient algorithm to actually
perform the motion. For example, after determining that a sphere can be distanced along a
line from a set of other spheres if that line does not intersect the contour of the object
formed by unifying all the other spheres, it is a not obvious how to mathematically
represent that contour. One may wish to determine the shortest path (without collisions)
relative to distance or time in directing a robot through a set of obstacles.
DEFINITIONS
Two objects collide if their interiors intersect.
N.B. In all the definitions and theorems below, it will be assumed that,
initially the interiors of the objects of any collection are pairwise disjoint. (i.e.
Their boundaries may intersect.)
A body B is said to be moveable relative to a collection of bodies {Oa} if it is possible to effect a continuous sequence of rigid
motions {f(t): 0<=t<=1} with f(0)=B, f(1) is not= B and for all a
and for all t, the interiors f(t) and Oa do not
intersect. If, in addition, for all d>0, there exists a continuous family of rigid
motions {f(t):0 <= t <= 1}
with f(0) = B and distance {f(1), B}>= d, B is said to be moveable
to infinity.
 |
 |
Moveable objects not moveable to infinity |
Moveable objects moveable to infinity |
A collection of bodies {Bi}1 <= i <= n is movably separable if there exists a sequence
of rigid motions such that for each pair of distinct k and l: 1<=k,l<=n, for each
d>0 eventually distance {Bk, Bl}>d.
A collection of bodies {Bi}1 <= i <= n is interlocked if it is not movably separable .
A collection of bodies {Bi}1 <= i <= n is sequentially separable if for all k:
1<=k<=n, Bk is moveable to infinity relative to {Bi}-Bk.
As the diagram below illustrates, a collection of bodies can be movably separable without
being sequentially separable.
 |
 |
Objects sequentially separable |
Objects moveably separable but not sequentially
separable |
A collection of bodies {Bi}1 <= i <= n is simultaneously movably separable if it is
interlocked but the bodies can still be separated by moving subsets of {Bi}1
<= i <= n
simultaneously. (Each such subset includes at least two bodies) The fact that such
collections of objects exist is illustrated by the diagram below and our applet.
 |
Objects simultaneously moveable separable |
A collection of rectangles is isothetic if each of their sides is parallel to a
coordinate axis.
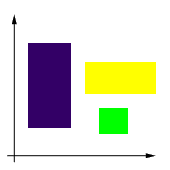 |
A collection of isothetic rectangles |
A polygon P is described as simple if the only points of the plane that belong to
exactly two edges are the vertices of P and no points of the plane belong to more than two
edges.
A simple polygon is monotone with respect to a line L if for every line m
perpendicular to L the intersection of the polygon with m is connected, i.e. the
intersection must be a line segment, a point, or empty.
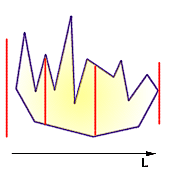 |
Monotone polygon |
If we can find a point x0 in a solid body B such that for all x in B, the
line joining x0 and x is wholly in B, B is star-shaped about x0.
The set of such x0 is called the kernel of B.
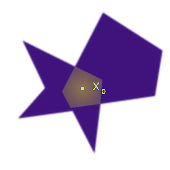 |
Star shaped polygon
x0 is one of the points of the kernel. It can see any other point inside of the
polygon. |
If for all points x and y in a solid body B, the line joining x and y is wholly in B, B is
convex. Note that convex bodies are star-shaped about all their points and monotone
in every direction.
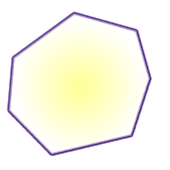 |
Convex polygon |
An n-sided simple polygon is star-shaped if n <= 5 and
convex if it is a triangle. (The first observation was employed in the
design of our applet to ensure that the objects the user creates are star-shaped. Neither
assertion admits a converse.)
The convex hull of a set of points is the intersection of all possible convex
objects which contain them.
Consider a problem of separating circles in sequence using translations along a certain
direction L. One of the approaches is to sweep a line perpendicular to L from infinity.
The first circle whose center is completely crossed by the sweeping line can be moved to
infinity (circle 1 in the picture). The algorithm is then applied to the remaining
circles. The fact that the sweeping line crosses the center of a circle guarantees an
empty corridor whose width is equal to the circle's diameter.
Next, consider the problem of separating isothetic rectangles along a specified line L.
(L need not be parallel to a coordinate axis) A somewhat different approach may be
suggested. Construct a line of support (see the diagram below) for each rectangle
perpendicular to L. This line of support intersects rectangles A,B,C, and D at the support
vertices a,b,c, and d, respectively. One might suggest that an ordered sets of
translations can be obtained by sorting the projections of the support vertices on L. It
works fine for rectangle B . However, it fails to translate rectangle D, since the latter
is blocked by rectangles A and C although the projection of its support vertex comes
second in the list. Hence this method does not work.
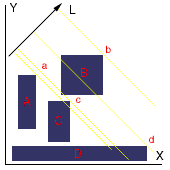 |
Lines of support a,b,c, and d for isothetic
rectangles A,B,C, and D respectively |
The following method of finding the first rectangle that can be moved in the direction
given can also be applied to translating any set of monotonic polygons in a specified
direction. Given a set of rectangles and a direction in which they are to be translated
consider two sides of each rectangle which intersect at the support vertex. The two line
chain formed by these sides consists of 3 vertices. Rotate the axes such that the X-axis
is parallel to the direction of translation . The top vertex is the one that has the
largest Y-coordinate relative to the direction of translation . Next imagine that the set
of chains is illuminated by a light bulb positioned at infinity. We assert that the chain
with lowest illuminated top vertex can be moved first in a specified direction. Indeed,
were this not true, (i.e. there is another 2-side chain obscuring the selected chain),
then that chain would had the lowest illuminated top vertex.
To determine the translation ordering of a set of any monotonic polygons, start by
isolating a chain of each polygon bounded by the top and bottom vertex (relative to the
direction of translation). This can be done by bringing parallel lines of support from
plus infinity and minus infinty in the direction perpendicular to L until each line
ecounters the first vertex of the polygon on either side. The line sweeping from the top
encounter the top vertex, and the one sweeping from the bottom encounters the bottom
vertex. These two vertices divide the polygonal chain into two subchains. Consider the
subchain whose vertices have a higher X-coordinate relative to L. Illuminate the obtained
subchains with a light source coming from infinity parallel to L. The subchain with the
lowest illuminated top vertex can be translated in direction L. Proceed in the same manner
for the remaining subchains.
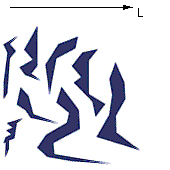
|
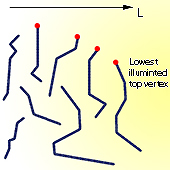
|
A set of polygons to be translated in direction
L |
Illuminated right polygonal chains. The polygon
with the lowest illuminated top vertex can be moved in the direction L |
Theorem 1 (Robert Dawson 1984)
In any collection of m balls in Rn, there exist at least min{m,n+1} balls
which are movable to infinity .
The above result was strengthened by Professor Toussaint.
Theorem 1 A (Godfried Toussaint 1984)
Consider a collection of balls {Bi} in Rn. Let h (h <= r) be the number of centres of those balls which lie on either
the vertices, edges or faces of the convex hull of {Bi}. Then at least h of the
balls are moveable to infinity.
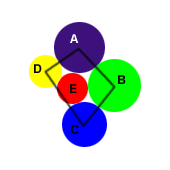 |
Balls A, B, C, and D are moveable to infinity |
Theorem 2 (Robert Dawson 1984)
In any collection of at least three smooth convex bodies in R2, at least
three elements are movable.
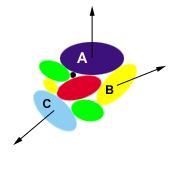 |
Objects A, B, and C are moveable to infinity |
This theorem, however, is not necessarily true for R3 . Below is a picture
of a convex tile (undergoing rotations around the vertical axis clockwise) which if
connected with similar tiles cannot be pushed out or pushed in. There exists a
configuration of 12 such tiles, such that there is not a single tile which may be moved
without disturbing the others.
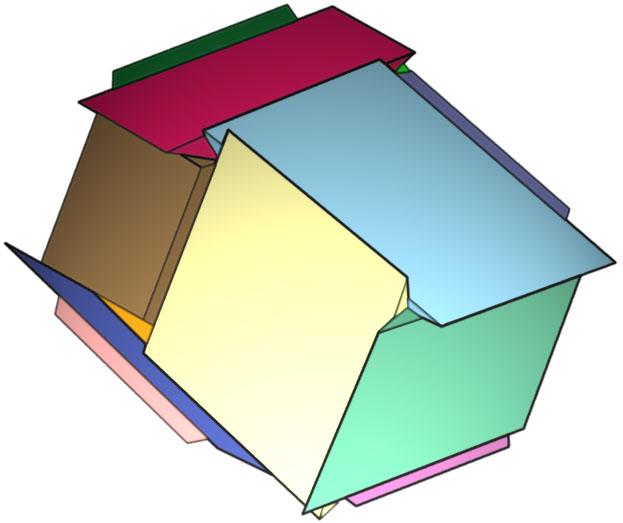
|
Twelve convex tiles, such that there is not one
which may be moved without disturbing the others |
Theorem 3 (Robert Dawson 1984)
Any collection {Bi}1 <= i <= 1 of star-shaped objects in Rn is
simultaneously movably separable.
EXAMPLES OF PUZZLES (Prof. Toussaint separates objects using a sequence of
rotations and translations)
Click here for BOMB APPLET
REFERENCES
(1) R.J. Dawson, ''On removing a ball without disturbing the others ,'' Mathematics
Magazine, vol57, no1, January 1984, pp27-30.
(2) G.T. Toussaint, ''On translating a set of spheres'', Technical Report SOCS-84.4,
School of Computer Science, Mcgill University, March 1984.
(3) G.T. Toussaint, ''Moveable Separability of Sets'', Technical Report No. SOCS-84.17,
School of Computer Science, Mcgill University, November 1984.
USEFUL LINKS
(1) Mobility of objects
in space
(2) Jack Snoeyink's
sculpture
SPECIAL THANKS TO
Godfried
T. Toussaint for providing the examples of the puzzles.
|



