What is it?
The Cauchy-Schwartz Inequality |<U,W>| ≤ ||U||∙
||W|| is an example of a lemma.
"Lemma" is Latin for "unimportant
theorem".
( Not exactly: a
lemma is a result which is needed to prove a more general or harder theorem .)
Where did it come from?
We can visualize it and explore its origin at the same time.
Let's start with the assumption that the shortest distance
between two points on a flat (See Note 1) surface is a straight
line.
In the diagram, it's a shorter walk from O to B, than from O
to A and then from A to B.
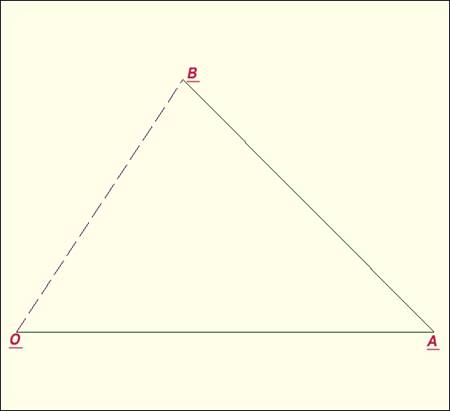
(By the way, the diagram was generated using Calgraph, a Graphing/Statistics/Calculus Calculator created
by Kishore Anand. You can download it at http://math-interactive.com/download.html
and run it on any Windows laptop or desktop.)
Let's call the vector joining O to A: U =
(u1 , u2).
Similarly, after reaching the point A, we walk parallel to
the vector W = (w1 , w2).
(Line 1)
If we walked directly from O to B,
we would be at the point with coordinates: (u1
+ w1 , u2 + w2).
So, translating our statement about the shortest distance
between two points being a straight line into vector algebra, ||U + W|| ≤ ||U|| + ||W||
Since all the quantities are non-negative, the preceding
inequality is still true if we square it. (The reason to square it is to avoid
having to deal with square roots.)
|| U + W ||2 ≤
( ||U|| + ||W||)2
||(u1 + w1
, u2 + w2)||2 ≤
||U||2+ ||W||2 + 2||U|| ∙||W||
(u1 + w1)2+(
u2 + w2)2 ≤
||( u1 , u2)||2+|| (w1 , w2)||2
+ 2 ||U||∙ ||W||
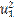 +
+
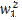 +
2 u1 w1 +
+
2 u1 w1 + 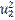 +
+ 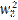 +2 u2
w2 ≤ ||( u1 , u2)||2+||
(w1 , w2)||2 + 2||U||∙ ||W||
+2 u2
w2 ≤ ||( u1 , u2)||2+||
(w1 , w2)||2 + 2||U||∙ ||W||
Rearranging the terms on the left side:
(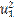 +
+
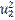 )
+ (
)
+ ( 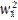 +
+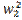 )
+ 2 u1 w1 + 2 u2 w2 ≤
||( u1 , u2)||2+||
(w1 , w2)||2
+2 ||U||∙ ||W||
)
+ 2 u1 w1 + 2 u2 w2 ≤
||( u1 , u2)||2+||
(w1 , w2)||2
+2 ||U||∙ ||W||
On the left, the
terms in parentheses are exactly ||( u1 , u2)||2 and ||(w1 , w2)||2 respectively.
Subtracting them from both sides and then dividing everything by 2 we have:
u1 w1+
u2 w2 ≤ ||U||
∙||W||
But the left is exactly the dot or inner product < U, W > of the two
vectors U and W , so we have:
|< U, W >| ≤ ||U||
∙||W|| (Line 2)
(If you are unsatisfied, see Note 2.)
Who needs it?
The
following three applications can be
proved in one of two ways: directly or
by showing that the relations live in a normed vector space, so that they derive from the general
Cauchy-Schwartz Inequality. However, either type of proof demands a
knowledge of subjects traditionally taught after Vector Algebra. (Quantum
Mechanics, Integration and Infinite
Series).
1 Physics: Arguably,
the most important tenet of Quantum Mechanics is a direct
consequence of the Cauchy-Schwartz Inequality:
The Heisenberg
Uncertainty Principle: There
is a fundamental
limit to the precision to which certain pairs of physical quantities of a particle
can simultaneously
be measured.
e.g. A
particle's position x and momentum p:
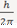 ≤
∆x ∙∆p
≤
∆x ∙∆p
For example, the more accurately the position
is measured (∆x small), the greater
will be the uncertainty in the momentum (∆p),
as the product of the two errors must be at least  .
.
An elegant, fairly simple proof on the Uncertainty
Principle appears here:
http://www.phys.ufl.edu/courses/phy4604/fall18/uncertaintyproof.pdf
2 If f and g are integrable
functiona over domain E: (f* is the complex conjugate
of f)
|∫E f*g dx| ≤
( ∫E | f |2 dx)1/2 ( ∫E |g|2 dx)1/2
3 (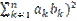 ≤
≤ 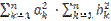
Taking the limits of both sides as 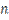 →∞, this inequality
can be used in convergence proofs.
→∞, this inequality
can be used in convergence proofs.
(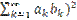 ≤
≤ 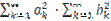
Here's the skeleton of a proof by Mathematical
Induction:
The Verification Step will start
with n = 2
(The n=1 case is trivial and the Algebra for the n=2 case is instructive for the Induction Step.)
We will need: 0 ≤ 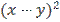 =
= 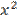 +
+ 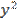 - 2
- 2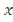
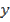
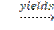 2
2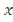
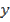 ≤
≤ 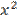 +
+ 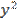 (Line 3)
(Line 3)
(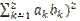 =
= 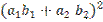 =
= 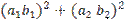 +2
+2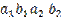
≤ 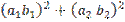 +
+ 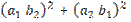 = (
= ( 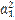 +
+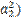 (
( 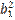 +
+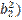 =
= 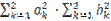
(The inequality comes
from replacing x by 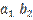 and y by
and y by 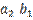 in (Line 3).
in (Line 3).
The Induction Step can be accomplished with
analogous algebra to the last few lines.
How do you know it's valid?
The general proof is constructive, in other words, a cute trick.
U and W are vectors
in an Inner Product Space over a field F.
(See Note 3)
Consider U- α W (where
α ε F)
We will assume that W ≠
0
as that case is trivial.
(Line 4)
0 ≤ < U- α W, U- α W >
(true
for the inner product of any vector with itself, equality only for 0)
Expanding the left hand side:
<U, U-
α W > - α <W,
U- α W >
= <U, U> - α *<U,
W> - α <W, U>
+ α∙ α*
<W, W>
Set α = 
(No worries about a 0 denominator as W was assumed to be a non-zero vector.)
0 ≤ < U-
α W, U- α W >
=
<U, U> −  <U, W>
-
<U, W>
- 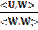 <W,
U> +
<W,
U> + 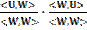 <W, W> (Line 4)
<W, W> (Line 4)
Simplifying the preceding
line:
0 ≤ <U, U> - 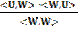
A little Algebra and the realization that 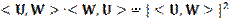 and <U,
U> =
and <U,
U> = 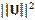
yields 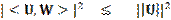
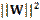
or simply: |<U, W>| 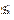 ||U||
∙ ||W||
( Line 5)
||U||
∙ ||W||
( Line 5)
Incidentally, tracing back to close to the beginning of
the proof ( Line 4), we have equality if
and only if U = α W, so equality occurs only when U
and W are linear multiples.
i.e.
In 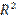 or
or 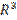 equality occurs in the Cauchy-Schwartz
Inequality (Line 5) only if U and W are parallel
vectors.
equality occurs in the Cauchy-Schwartz
Inequality (Line 5) only if U and W are parallel
vectors.
Notes:
1) By normal, flat 2-dimensional space, we mean the surface
of a piece of paper as opposed to the curved 2-dimensional surface of, for
example, a sphere or a bagel.
In real two dimensional real space, the inner product is the
same as the dot product of two vectors.
So if U = (u1 , u2) and W = (w1 , w2)
<U, W> = U ∙ W = (u1 , u2) ∙ (w1
, w2) = 2 u1 w1 + 2
u2 w2
2) The eagle-eyed reader might have noticed a hole in the
proof. The absolute value in Line 2 wasn't
justified. However, if, after Line 1, point B had been taken as (u1 - w1 , u2 - w2), then proceeding analogously, the left side of Inequality I would have had
been multiplied by -1 . Thus, the absolute
value at Line 2 can be justified.
3) Definition of an Inner Product Space.
An inner product space is a vector space V over a field F (F
= R or C) together with an operation <. , .>
<. , .>: VxV -> F
(The idea is that the inner product is a function with two
vectors as the input and a single real or complex number as the output.)
·
Conjugate symmetry:
<U, W> = <U, W>C
{\displaystyle
\langle x,y\rangle ={\overline {\langle y,x\rangle }}}
·
Linearity in the first argument:
< αU,w>
= α <U,W>
<U + V,W> = <U,W> + <V,W>{\displaystyle
{\begin{aligned}\langle ax,y\rangle &=a\langle x,y\rangle \\\langle
x+y,z\rangle &=\langle x,z\rangle +\langle y,z\rangle \end{aligned}}}
·
Positive Definite: <U,U> ≥ 0 with
equality only if U is the
0 vector.
4) Sometimes, Mathematicians develop abstract systems for
their own amusement and are surprised or even miffed when their work proves
useful. For example, Group Theory was unknown outside pure Mathematics from its
inception circa 1855 until 1920 when Weyl rolled it
into Quantum Mechanics. Inner product spaces are generalizations of our
familiar R2 and,
as one can see from the applications of just this Inequality, have proved to be
extremely useful.



